LES MACLES
LES MACLES
5.1.4. Macles par pseudosymétrie (1)(fig. 20)
Dans ce cas, l’obliquité n’est pas nulle. Les macles sont souvent dues à des cristallisations appartenant à des systèmes de plus faibles symétries mais avec des paramètres proches de sous-multiples de systèmes cristallins de plus hauts degrés de symétrie : ainsi l’exemple de l’albite triclinique pseudo monoclinique, ou de cristaux orthorhombiques pseudo quadratiques.
Elles apparaissent si le réseau simple ou multiple possède une symétrie approchée qui n’appartient pas au cristal et, plus généralement, s’il existe des plans et rangées suffisamment denses, donc d’indices de Miller simples, qui se trouvent être à peu près perpendiculaires. Tout plan de symétrie admettra une rangée pseudo-perpendiculaire.


Fig. 19 : Macle de la fluorine
(Illinois 4 cm et Derbyshire 15 mm)
Dans le cas d’un plan de macle, l’angle entre la normale au plan et la rangée pseudo perpendiculaire définira l’obliquité de la macle. La mise en évidence d’une macle reviendra donc à rechercher dans le réseau une rangée suffisamment proche de la normale au plan. Le réseau, simple ou multiple, de l’un des individus, se prolonge approximativement dans l’autre, mais les cristaux maclés ont exactement en commun le plan ou l’axe de pseudosymétrie qui sert de plan ou d’axe de la macle. Dans les macles par pseudosymétrie, la surface d’accolement ne peut pas être quelconque ; l’accord entre les deux réseaux ne pouvant se faire que dans le plan d’accolement : macles par contact
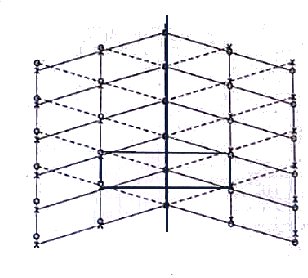
Fig. 20 : Macle par pseudosymétrie
Exemples :
FELDSPATHS
Tout d’abord, permettez-moi de vous renvoyer au paragraphe 6, qui présente de manière très détaillée les macles des feldspaths.
ALBITE
L’albite cristallise dans le système triclinique (le plus pauvre en éléments de symétrie), mais avec des paramètres très proches de ceux du système monoclinique, de sorte que l’on peut observer un maclage pseudo symétrique grâce à ces faibles différences.
Ainsi, le plan (010) est plan de pseudosymétrie et la rangée [010] axe de pseudosymétrie. Cette rangée et ce plan sont pseudo perpendiculaires, et on peut décrire la macle comme s’opérant par rotation binaire autour de [010] aussi bien que par réflexion sur (010). Les deux possibilités sont géométriquement équivalentes, mais seul l’un des deux éléments est rigoureusement commun à deux cristaux.
D’où deux types de macle (fig. 21) :
C’est le plan (010) qui est commun et joue le rôle de plan de macle. L’association s’effectue alors par contact sur ce plan ;
C’est la rangée [010] qui est commune et joue le rôle d’axe binaire de macle. L’accolement se fait selon un plan " de section rhombique ", qui n’est pas un plan réticulaire mais qui contient notamment la rangée [010].

Fig. 21a : Macles de l’albite et du péricline

Fig. 21b : Macles de carlsbad et du péricline dans orthose (Issoire)
Autres exemples
Les macles par pseudo symétrie sont les plus abondantes, on les observe par exemple dans les cristaux orthorhombiques pseudo hexagonaux (macle sur {010}) : aragonite, barytine, cérusite, marcassite, chrysobéryl, bournonite, etc ; toutes sont de faciès très différents (cf paragraphe 6)
5.1.5. Macles par pseudo mériédrie (fig. 22)
Lorsque la maille élémentaire possède une symétrie approchée supérieure à sa symétrie vraie, on est en présence d’une macle par pseudo mériédrie.

Fig. 22 : Réseaux dans le cas d’une macle par pseudomériédrie
Les réseaux tricliniques pseudomono-cliniques ou monocliniques pseudoorthorhom-biques en sont de bons exemples (2). Le réseau ne se prolonge pas rigoureusement d’un individu à l’autre, et apparaît une certaine obliquité entre les deux individus.
5.1.6. Macles par pseudo mériédrie réticulaire (fig. 23)
Lorsque c’est la maille multiple qui a une symétrie approchée, les coïncidences de positions atomiques sont encore moins nombreuses, et la macle un peu plus improbable :on l’appelle alors macle par pseudo mériédrie réticulaire.
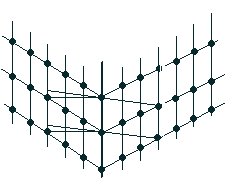
Fig. 23 : Macle par pseudomériédrie réticulaire (pyroxènes monocliniques)
Le principe en est schématisé figure 20, avec l’exemple de la macle (001) des pyroxènes monocliniques. Ce sont des particularités de dimensions de la maille élémentaire qui sont responsables de la pseudosymétrie.
Exemples
CHALCOPYRITE
La maille de la chalcopyrite, quadratique, est presque deux fois plus haute que large, et quatre mailles associées pourront donc avoir une symétrie grossièrement cubique. La chalcopyrite présente ainsi, en plus des macles du système quadratique, des macles typiques du système cubique.
QUARTZ
Le quartz, pour ces macles du Japon et de la Gardette (fig. 24) possède également une pseudo-symétrie quadratique d’une maille multiple.
Le plan d’accolement est (11.2) et les individus forment un angle de 84°33’, proche mais différent de 90°C, l’obliquité n’est donc pas nulle.



Fig. 24 : Macle de la Gardette et du Japon pour le quartz (échantillons chinois (3x3 cm2 et 10x8 cm2)
Autres exemples
Pour des indices de macle faible (maille multiple pas trop grande), les exemples sont assez nombreux : macle des pyroxènes monocliniques, macle de Carlsbad, macles de la staurolite, du rutile), macle des carbonates orthorhombiques pseudo hexagonaux (cérusite, aragonite)









