LES MACLES

LES MACLES LES MACLES

5.1.2. Macles par mériédrie

Les macles par mériédrie que l’on appelle également Groupe de Complément et dont l’interprétation est due à Bravais, intervient, comme le nom l’indique, uniquement pour des cristaux mérièdres.

Ces cristaux sont alors moins symétriques que leur réseau, et la macle tend à accroître la symétrie, vers l’holoédrie dont découle la méri-édrie des deux individus.

Dans ce cas, le réseau secondaire de la macle est confondu avec le réseau des deux individus. L’indice de la macle est ainsi égal à 1, et l’obliquité est nulle.

Fig. 9 : Défaut d’empilement dans la structure du diamant

Le plan hachuré est un plan miroir

En outre, si la mériédrie est d’ordre n, il existe n orientations possibles du cristal, symétriques les unes par rapport aux autres, ce qui conduit effectivement à une superposition parfaite du réseau, mais les éléments de symétrie de la macle se trouvent parmi ceux du réseau que l’on n’observe pas sur le cristal.

Ce type de macle par mériédrie peut être difficile à discerner par une simple observation. En effet, si les cristaux possèdent déjà une symétrie holoèdre, la macle demeurera interne au volume du cristal et la macle ne sera pas macroscopiquement décelable. Ainsi, un cube peut receler des macles par mériédrie sans que l’on puisse les détectées.

Les figures 9 et 10 présentent comment peut intervenir les macles par mériédrie non discernables macroscopiquement. Ces macles sont définies par une superposition parfaite entre le réseau des individus et celui de la macle. Ainsi, par exemple, à partir de la structure du diamant (fig. 9), on peut observer un défaut d’empilement de gauche à droite. Si l’on fixe une chronologie de genèse cristalline selon l’axe oy (gauche à droite sur la feuille). On observe un empilement abcdedcba, qui créera une macle selon le plan miroir e, mais qui ne sera pas observable macros-copiquement puisque le réseau cfc est maintenu.

Fig. 10 : Macle par mériédrie

AA’ : plan de macle

BB’ : surface limite des cristaux quelconques

Il est de même sur la figure 10, où l’on a simulé une quelconque géométrie limitée dans la maille élémentaire. Lors de l’empilement des atomes, ions ou molécules, il arrive que tantôt intervienne le motif à pointe en haut à gauche, tantôt celui à pointe en bas à droite (comme pour des carreaux de faïence (1) qui seraient posés dans un sens ou dans l’autre.

La surface d’accolement peut alors être quelconque conduisant à un faciès de pénétration. Elle peut être plane et conduire à une macle par contact, ou bien même être parfaitement quelconque, et à la limite ne former qu’un mélange isomorphe de plusieurs orientations d’un même cristal comme c’est le cas si l’on considère l’ensemble de la figure 10.

En revanche, s’il s’agit de formes affectées géométriquement par l’holoédrie pentagone, scalénoèdre...), alors il y aura formation de macles par pénétration, et l’on pourra distinguer aisément les deux individus de la macle.

Remarque :

Pour satisfaire aux minimisations des énergies, les macles sont souvent dues à des défauts d’empilement miroirs.

Exemples :

PYRITE

La pyrite (1) cristallise dans l’hémièdre centrée du système cubique de symétrie 3A₂/3M 4 A₃ C

inférieure à celle de l’holoédrie 3A₄/3M 4A₃ 6A’₂/6M' C.

Il y a deux orientations possibles du cristal par rapport au réseau. Les éléments de symétrie qui manquent à la pyrite sont donc 3A₄, 6 A’₂, 6 M’. Pour passer d’un individu à l’autre, on peut adopter indifféremment l’un quelconque de ces éléments géométriques équivalents : rotation de 90° autour de l’un des A₄, réflexion sur l’un des 6M’..., sont des opérations identiques pour décrire la fameuse macle en croix de fer de la pyrite.

Cette dernière est obtenue par interpénétration de dodécaèdres (fig. 11), affectés par l’hémiédrie et donc clairement identifiable.

Dans la variété triglyphe de la pyrite, les stries visibles sur les faces sont dues à l’alternance des arêtes du dodécaèdre. Elles définissent donc la macle en présentant des domaines où les stries d’une même face sont divergentes, correspondant aux deux orientations rectangulaires possibles.

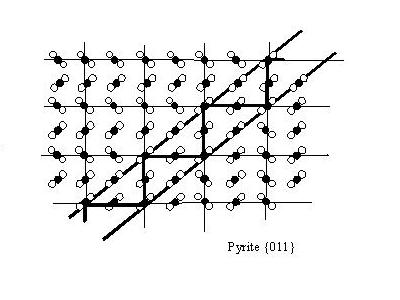
Fig. 11a : macle en croix de fer de la pyrite

Morphologie et structure- photo Le monde des cristaux , V de Michele

Fig. 11b : Pyrite triglyphe (10mm) -- Fig. 11c : octaèdres de pyrite maclés (Pérou)

QUARTZ

Pour les cristaux tétartoèdres, il y a quatre orientations possibles du motif cristallin dans le même réseau. Le quartz a en est un on exemple. Le recensement des diverses associations conduit à plusieurs types de macles qui, notamment, modifient les propriétés physiques (pouvoir rotatoire et piézo-électricité). On distingue ainsi la macle du Dauphiné, ou macle électrique, celle du Brésil, ou macle électro-optique, et la macle optique.

Les macles dites par transformation, sont généralement mieux connues, certainement parce que l’un des meilleurs exemples des minéraux comportant ce type de macle est le quartz. De nombreux minéraux cristallisent sous différentes phases en fonction de la température. Ainsi, si l’une de ces espèces commence à cristalliser dans sa phase haute température, lors du refroidissement interviendra par la suite la cristallisation de la phase basse température. Or, généralement les distances interatomiques sont voisines d'une phase à l'autre. Ainsi, si le degré de symétrie de la phase basse température est inférieure à celle de haute température, comme c’est généralement le cas, elle se maclera en respectant la forme cristalline originelle.

Macles de transformation polymorphique

La plupart des matériaux possède à haute température une structure à haut degré de symétrie, c’est à dire avec de nombreux éléments de symétrie. Principalement dues à des effets de compacité permis par l’agitation thermique, il s’agit là principalement de structures de type hexagonal ou cubique. A plus basse température, les liaisons interatomiques sont plus fortes car moins soumises à cette agitation thermique, de sorte que les orientations de ces liaisons vont tendre vers des positions d’équilibre (cf fig.2), dans des structures de moindre degré de symétrie (quadratique, rhomboédrique, monoclinique...).

Ainsi, lorsqu’un minéral passe à l’état solide d’une phase haute température A, à une phase de plus basse température B, il y a ce que l’on appelle transformation polymorphique.

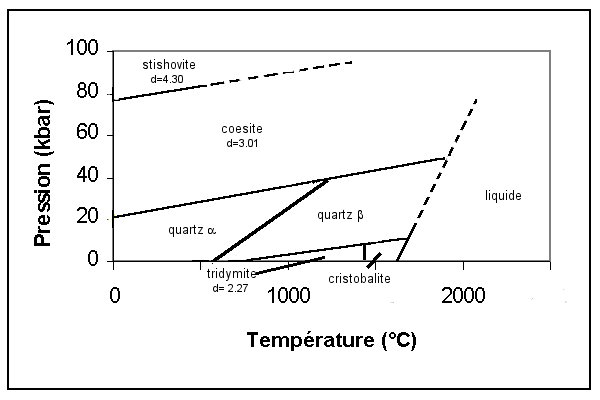
Fig. 12 : pseudomorphisme du quartz responsable du maclage

diagramme température-pression d’existence des différentes phases de la silice

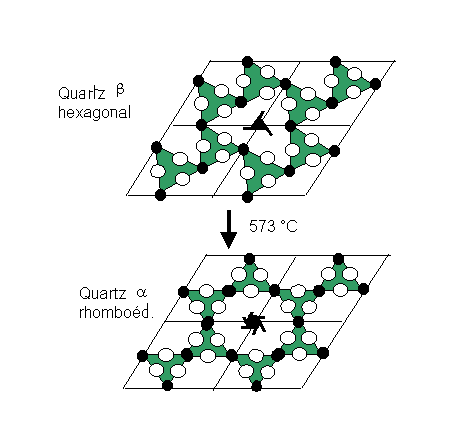
Polymorphisme : passage du quartz b au quartz a

Respect de la structure haute température hexagonale Apparition d’un axe sernaire

Pour le quartz, cette transition quartz a – quartz b intervient à 573°C. Le quartz qui cristallise dans sa phase b hexagonale à haute température, cristallise dans sa phase a rhomboédrique pour des températures inférieures. Il en résulte la formation de macles, généralement de la macle dite " du Dauphiné ", plus rarement de celle du Brésil ou encore une combinaison des deux.

C’est ainsi que les cristaux de quartz formés à haute température ; comme ceux des Alpes, présente un faciès basés sur des prismes hexagonaux, alors que leur structure interne, quant à elle , appartient au système rhomboédrique..

Il en est de même pour la leucite, cubique au-dessus de 560 °C, qui devient quadratique en deçà de cette température, pour la wurtzite qui se transforme en blende à 1 024°C, la pyrite qui devient marcassite à 400°C, l’analcime, les grenats...

Autres exemples :

- Restauration d’un centre de symétrie : wulfénite, topaze, tourmaline, hémimorphite..

- Restauration des axes 4 : pyrite, chalcopyrite, cuivres gris...